trabajo mates funciones

Clasificación de triángulos según sus lados

triangulo equilatero

Si sus tres lados tienen la misma longitud (los tres ángulos internos miden 60 grados).

imagen

Triángulo isósceles

Si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida.
imagen

Triángulo escaleno

Si todos sus lados tienen longitudes diferentes. En un triángulo escaleno no hay ángulos con la misma medida.
imagen

Clasificación de triángulos según sus ángulos

Triángulo Rectángulo

Si tiene un ángulo interior recto (90 grados)

. A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
imagen

Triángulo obtusángulo

Si uno de sus ángulos es obtuso (mayor de 90); los otros dos son agudos (menor de 90

Triángulo acutángulo

Cuando sus tres ángulos son menores a 90 grados; el triángulo equilátero es un caso particular de triángulo acutángulo.
imagen

Triángulo equiángulo

Normalmente se llama Triángulo equilátero y ya se ha comentado anteriormente.

Propiedades de los triángulos

tenemos las siguientes características:

Triángulo acutángulo isósceles: con todos los ángulos agudos, siendo dos iguales, y el otro distinto, este triángulo es simétrico respecto de su altura diferente.
Triángulo acutángulo escaleno: con todos sus ángulos agudos y todos diferentes, no tiene ejes de simetría.

Los triángulos rectángulos pueden ser:

Triángulo rectángulo isósceles: con un angulo recto y dos agudos iguales (de 45 cada uno), dos lados son iguales y el otro diferente, naturalmente los lados iguales son los catetos, y el diferente es la hipotenusa, es simétrico respecto a la altura que pasa por el ángulo recto hasta la hipotenusa.
Triángulo rectángulo escaleno: tiene un ángulo recto y todos sus lados y ángulos son diferentes.

Los triángulos obtusángulos son:

Triángulo obtusángulo isósceles: tiene un ángulo obtuso, y dos lados iguales que son los que parten del ángulo obtuso, el otro lado es mayor que estos dos.
Triángulo obtusángulo escaleno: tiene un ángulo obtuso y todos sus lados son diferentes.

Acutángulos:

Rectángulo:
imagen

Obstusángulo:
imagen

Incentro

El incentro es el centro de la circunferencia inscrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma (el radio de dicha circunferencia). Más concretamente, es el punto de intersección de las bisectrices de cada uno de los ángulos del triángulo (siendo una bisectriz la recta que divide a un ángulo en dos ángulos iguales), por lo que para representarlo gráficamente debemos dibujar las tres bisectrices y localizar el punto de intersección de las mismas. En la imagen siguiente podéis verlo:
- Circuncentro
  
  El circuncentro de un triángulo es el centro de la circunferencia circunscrita al triángulo, por lo que la distancia a cada uno de sus vértices es la misma (el radio de dicha circunferencia). En concreto, es el punto de intersección de las mediatrices del triángulo (siendo una mediatriz la recta perpendicular a un lado que pasa por el punto medio del mismo). Por tanto, para representar gráficamente el circuncentro dibujamos las tres mediatrices y localizamos el punto de intersección de las mismas. Puede verse el circuncentro de un triángulo en la siguiente imagen:
Ortocentro

El ortocentro de un triángulo es el punto de intersección de las tres alturas del triángulo (siendo una altura el segmento que parte de un vértice y es perpendicular al lado opuesto a dicho vértice). Entonces para representar gráficamente el ortocentro de un triángulo dibujamos las tres alturas y nos quedamos con el punto en el que se intersecan. En esta figura puede verse el ortocentro de un triángulo:

EL TEORME DE PITAGORAS

El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos. Es la proposición más conocida entre las que tienen nombre propio en la matemática.

TEOREMA DE PITAGORAS

EN 3D!!!


Esto es una representacion grafica en 3D de el teorema de pitagoras.

EL TEOREMA DE TALES
teorema en el problema del arbol y su sombra

El objeto es vertical y su sombra horizontal. La inclinación de la luz del sol será la que determine la longitud de la sombra. Con el punto más alto del objeto, el punto donde éste llega al piso y el punto más lejano de la sombra, armamos un triángulo imaginario.

Nominamos los vértices con las letras A, B y C.

Tenemos que averiguar cuanto mide el lado AB, que por ahora será igual a X.

Medimos la longitud de la sombra, que es el lado BC. Supongamos que tiene 21.36 metros.

Con ese dato todavía no podemos calcular X.

El paso siguiente es tomar un referente de un metro de altura (A’B’) y medir su sombra (B’C’). Supongamos ahora que la sombra de éste objeto es igual a 1.78 metros. Esto se tiene que hacer enseguida de medir la primera sombra, para que no haya una variación en el ángulo de la luz solar.

Lo que hicimos no fue otra cosa que construir un triángulo semejante al primero, pero con la diferencia que sabemos dos datos: las medidas de los catetos.

Por relación de triángulos semejantes sabemos que AB/BC = A’B’/B’C’, y que expresado con valores es: X / 21.36 = 1.00 / 1.78

Entonces despejamos el valor de X, que saldrá de calcular: (21.36 × 1.00) / 1.78

X=12.00 metros.

Así de fácil.

Este cálculo no se modifica si el piso tiene pendiente. Pero si objeto estuviese inclinado, bastará con tener la precaución de ubicar nuestro referente de un metro con la misma posición para que el resultado sea el más aproximado posible.

LUGARES GEOMETRICOS

¿que es un lugar geometrico?:Un lugar geométrico es un conjunto de puntos que cumplen determinadas condiciones o propiedades geométricas,es complicada su aparicion en las figuras geometricas pero se produce con una simple formula:

MEDIATRIZ
La mediatriz de un segmento es la línea recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como el lugar geométrico — la recta — cuyos puntos son equidistantes a los extremos del segmento. También se le llama o se le denomina simetral.

Construcción gráfica de la mediatriz con regla y compas

BISEZTRIZ

La bisectriz de un ángulo es la semirrecta que pasa por el vértice del ángulo y lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de las semirrectas de un ángulo.

SECCION CONICA

Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

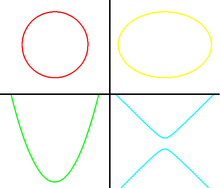secciones conicas

LA CIRCUNFERENCIA

La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro. Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo llamado centro.

LA ELIPSE:

método del jardinero:Esta construcción se basa en una técnica sintética mediante la cual se toma un hilo de longitud 2a que queda fijado por sus extremos en ambos focos.

Manteniendo el hilo tenso, se dibujará la elipse, ya que todo punto P de la figura verifica que su suma de distancias a los focos es constante y vale 2a (por ser la longitud del hilo).

Procedimiento:

Primero deben dibujarse perpendicularmente los dos ejes de coordenadas en el suelo y situar el eje Y en la dirección N-S, y el eje X en la dirección E-O.

Luego hemos de señalar los dos focos que están en el eje X a ambos lados del centro a una distancia c , es decir, en los puntos (c,0) y (-c, 0).

Después, con una cuerda que tenga de longitud l = 2a y colocando los extremos en los focos señalados, dibujar la elipse tal como se ve en la figura.

Resultado de imagen de la elipse metodo del jardinero

LA MESA DE BILLAR ELÍPTICA

Coloca la bola en el foco “F” e impúlsala con el taco en la dirección que quieras. Siempre entra en el agujero, salvo imperfecciones en la nivelación o excesivo efecto en la bola.

También entrará la bola si la lanzas desde otro sitio pero la haces pasar por el foco “F”.

En una elipse, las líneas que unen los focos con un punto cualquiera de la curva forman con ella (con su tangente) ángulos iguales. Luego si la bola viene por una de esas líneas, después de “reflejarse” en la curva seguirá por la otra línea y, por tanto, pasará por el otro foco. Ahí hemos puesto el agujero.

Resultado de imagen de mesa de billar eliptica

LA HIPÉRBOLA

Muchos tienen en sus casas esas lámparas con pantalla que se usan en los living-rooms o en la mesas de luz de las habitaciones, que al estar encendidas emanan un cono de luz hacia arriba y otro hacia abajo, los cuales forman sobre la pared dos figuras con forma de hipérbole.

Las figuras sobre la pared, formadas por la luz de la lámpara, se pueden reproducir experimentalmente tomando las medidas de cualquier lámpara del tipo que tengamos en casa y de su posición relativa a la pared. El siguiente gráfico muestra la geometría utilizada para tomar estas medidas:

– Se define como origen al filamento del foco o bombilla de la lámpara.

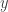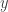– Los ejes $x$ e $y$ forman el plano horizontal con el eje $x$ paralelo a la pared y el eje $y$ perpendicular a la pared.

– El eje $z$ es el eje vértical.

Para desarrollar una descripción matemática de las figuras proyectadas por la lámpara sobre la pared, utilizando este sistema de coordenadas, es útil considerar a la luz que se sale por los extremos superior e inferior de la lámpara, como los círculos de dos conos simétricos respecto del eje $z$ con un origen común situado en el filamento del foco. Los dos conos de luz no son iguales e intersectan la pared en $y=D$ . El siguiente diagrama ejemplifica la idea:

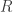La ecuación $\displaystyle (1)$ es la ecuación general para un par de conos circulares, simétricos respecto del eje $z$ , con punto en común al origen. Aquí $R$ es el radio de los conos cuando $\displaystyle z=\pm A$ ( $\displaystyle A$ es la distancia vertical desde el centro de la bombilla de luz hacia el circulo superior de la lámpara y hacia el círculo inferior de la misma).

$\displaystyle\frac{z^2}{A^2}=\frac{x^2+y^2}{R^2}$ $\displaystyle (1)$

$\displaystyle\frac {z^2}{(DA/R)^2}-\frac{x^2}{D^2}=1$ $\displaystyle (2)$

Las líneas formadas por la intersección de estos conos (la luz que sale de lámpara) con el plano (la pared) localizado en $\displaystyle y=D$ , generan las dos ramas de la hipérbola, definidas por la ecuación $\displaystyle (2)$ .

Los parámetros tanto del cono de luz superior como inferior, están dados en la descripción geométrica del problema y son los siguientes:

Cono Superior ( $\displaystyle A=A_t$ , $\displaystyle R=R_t$ ).

Cono Inferior ( $\displaystyle A=A_b$ , $\displaystyle R=R_b$ ).

Sustituyendo estos parámetros en la ecuación $\displaystyle (2)$ y resolviendo $\displaystyle z$ se obtienen las fórmulas para la luz reflejada por la lámpara, tanto por su extremo superior como por el inferior.

$\displaystyle z_{superior}=\frac{A_t}{R_t}\sqrt{x^2+D^2}$ $\displaystyle (3)$

$\displaystyle z_{inferior}=-\frac{A_b}{R_b}\sqrt{x^2+D^2}$ $\displaystyle (4)$

Tomadas las medidas experimentales versus lo calculado por las ecuaciones $\displaystyle (3)$ y $\displaystyle (4)$ se puede armar una planilla de cálculo, graficar los mismos y analizar la presición de las ecuaciones para replicar el fenómeno estudiado. En este caso consideramos los siguiente valores para los parámetros $\displaystyle D=22$ , $\displaystyle A_t=14$ , $\displaystyle R_t=15$ , $\displaystyle A_b=12$ y $\displaystyle A_t=20$ y obtenemos el siguiente gráfico:

LA PARÁBOLA

la antena parabolica

En las antenas satélites transmisoras, la así llamada parábola refleja las ondas electromagnéticas generadas por un dispositivo radiante que se encuentra ubicado en el foco del paraboloide. Los frentes de onda inicialmente esféricos que emite ese dispositivo se convierten en frentes de onda planos al reflejarse en dicha superficie, produciendo ondas más coherentes que otro tipo de antenas.

En las antenas receptoras el reflector parabólico se encarga de concentrar en su foco, donde se encuentra un detector, los rayos paralelos de las ondas incidentes.

Resultado de imagen de LA ANTENA PARABOLICA

EL HORNO SOLAR

el horno solar tiene la forma parabolica con la que capta toda la temperatura del sol que luego usa para transformarla en energia como un panel solar,el panel solar mas grande situado en francia suele llegar a temperaturas de 1000 a 4000 grados.

EL ESPEJO PARABÓLICO

¿Cómo se verían los objetos en un espejo parabólico?

Los rayos luminosos que parten de un punto, después de experimentar reflexiones en un espejo, vuelven a concurrir en otro punto que se denomina punto imagen. Una imagen puede ser real o virtual, la primera se forma con la convergencia de los rayos reflejados y puede recogerse en una pantalla; la imagen virtual se forma por las prolongaciones de los rayos reflejados y no se puede proyectar sobre una pantalla.

Vamos a llamar centro de curvatura al centro de la esfera que circunscribe exactamente a un espejo esférico o aproximadamente a un espejo parabólico. El foco siempre va a estar situado a loa mitad de distancia entre el centro de curvatura y el espejo.

Para trazar gráficamente la imagen de un objeto colocado ante un espejo seguiremos un método sencillo, trazamos tres rayos de los que conocemos su trayectoria:

Rayo 1: se traza desde la parte superior del objeto y se dibuja paralelo al eje, al reflejarse pasa por el foco.
Rayo 2: se traza desde la parte superior del objeto y se dirige al centro de curvatura, al reflejarse sigue la misma dirección.
Rayo 3: se traza desde la parte superior del objeto y se dirige al foco, al reflejarse sale paralelo al eje.

Según la distancia entre el objeto y el espejo la imagen es diferente. Consideremos un observador que se sitúa en distintas posiciones:

El observador está detrás del centro de curvatura. La imagen es real, invertida y más pequeña que él

Resultado de imagen de el espejo parabolico

MOVIMIENTOS EN EL PLANO

las traslaciones

¿que es un vector?

En física, un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo (o longitud) y una dirección (u orientación).¹ ² ³

En matemáticas se define un vector como un elemento de un espacio vectorial. Esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo y la dirección. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo. Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta

\mathbb {R}

, en el plano

\mathbb {R} ^{2}

, o en el espacio

\mathbb {R} ^{3}

Algunos ejemplos de magnitudes físicas que son magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan solo por su módulo que es lo que marca el velocímetro, en el caso de un automóvil, sino que se requiere indicar la dirección (hacia donde se dirige), la fuerza que actúa sobre un objeto, ya que su efecto depende además de su magnitud o módulo, de la dirección en la que actúa; también, el desplazamiento de un objeto, pues es necesario definir el punto inicial y final del movimiento.

Resultado de imagen de que es un vector?

Frisios

Un friso, palabra proveniente del Latín frisium,¹ sirve en arquitectura para denominar a la parte ancha de la sección central de un entablamento, que puede ser lisa o (en los órdenes jónico y corintio) estar decorada con bajorrelieves. En una pared sin columnas queda sobre el arquitrabe (‘viga principal’) y queda cubierto por las molduras de la cornisa.
Se llama pulvino al friso de sección convexa. Estos frisos fueron característicos del manierismo nórdico del siglo XVI, especialmente en la arquitectura de interiores y el mobiliario.

Decoración interior

En espacios interiores, el friso de una habitación es la parte de la pared sobre la moldura para cuadros y bajo las molduras del techo o la cornisa. Por extensión, un friso es una larga banda decorativa pintada, esculpida o incluso caligrafiada en ese lugar, por encima del nivel de los ojos. Los frisos decorativos pueden representar escenas en una secuencia de paneles separados. El material del que se fabrica el friso puede ser escayola, madera tallada o algún otro medio decorativo

Mosaicos

Un mosaico (del latín mosaĭcum [opus], ‘[obra] relativa a las Musas, artística’)¹ es una obra pictórica elaborada con pequeñas piezas de piedra, cerámica, vidrio u otros materiales similares de diversas formas y colores, llamadas teselas, unidas mediante yeso u otro aglomerante para formar composiciones decorativas geométricas o figurativas.

Cenefa

Cenefa (del árabe hispanizado «ṣanífa») es un adorno o elemento decorativo –generalmente cíclico, listado o repetido– usado en la arquitectura,¹ cerámica,² decoración y confección. Suele presentarse en forma de tira o franja alargada y estrecha sirviendo de marco, orla, perímetro, separación o borde.³ Cumple una función de contraste con el diseño del resto de la superficie donde se coloca.⁴ Puede aparecer como sinónimo de banda, festón (textiles), filete (marquetería), franja, greca, orla, repulgo (alfarería)
Areas y volumenes de figuras conocidas y menos conocidas

Áreas, perímetros y volúmenes de figuras geométricas

Áreas, perímetros y volúmenes de figuras geométricas

El globo terraqueo
Un globo es un modelo tridimensional representado sobre una esfera a escala de la Tierra (globo terrestre o globo geográfico) o de otro cuerpo celeste como un planeta o la Luna. Mientras que los modelos de distintos objetos se pueden hacer con formas arbitrarias o irregulares, el término globo se utiliza solo para los modelos de objetos que son aproximadamente esféricos. La palabra "globo" proviene de la palabra latina globus, significando una masa compacta de personas u objetos, y por extensión una esfera. Algunos globos terrestres incluyen relieve para mostrar montañas y otras características de la superficie de la Tierra.
También hay globos, llamado globos celestes o esferas astronómicas, que son representaciones tridimensionales de la esfera celeste, que muestran las posiciones aparentes de las estrellas y las constelaciones en el cielo.
Resultado de imagen de la esfera y el globo terraqueo

La esfera

En geometría, una superficie esférica es una superficie de revolución formada por el conjunto de los puntos del espacio que equidistan de un punto llamado centro.
Los puntos cuya distancia es menor que la longitud del radio forman el interior de la superficie esférica. La unión del interior y la superficie esférica se llama bola cerrada en topología, o esfera, como en geometría elemental del espacio.¹ Obviamente, la esfera es un sólido geométrico.
La esfera, como sólido de revolución, se genera haciendo girar una superficie semicircular alrededor de su diámetro.
Propiedades

Cualquier segmento que contiene el centro de la esfera y sus extremos están en la superficie esférica, es un diámetro.
Cualquier sección plana de una esfera es un círculo.
Cualquier sección que pasa por el centro de una esfera es un círculo mayor, y si la sección no pasa por el centro es un círculo menor.
Si se da un círculo de una esfera, los extremos del diámetro perpendicular a aquel se llaman polos de dicho círculo.

El método de Eratóstenes para calcular el diámetro de la circunferencia terrestre.

Una de sus principales contribuciones a la ciencia y a la astronomía fue su trabajo sobre la medición de la Tierra. Estando en la Biblioteca de Alejandría, encontró un informe de observaciones sobre Siena, ciudad situada a unos 800 Km. al sur de Alejandría, en el que se decía que el día del solsticio de verano (21 de junio) a mediodía, los objetos (como por ejemplo, los obeliscos) no producían sombra y en el fondo de los pozos podía verse la luz del sol. Esto se debe a que está ciudad está sobre la línea del trópico (en realidad, 33' al norte del Trópico de Cáncer)
Eratóstenes realizó observó que, en Alejandría, el mismo día y a la misma hora no se producía este mismo hecho. Asumió de manera correcta que el Sol se encontraba a gran distancia y que sus rayos, al alcanzar la tierra, lo hacían en forma (prácticamente) paralela. Esto ratificaba su idea de que la superficie de la Tierra era curva pues, de haber sido plana, no se hubiese producido esta diferencia entre las dos ciudades. El siguiente paso fue medir en Alejandría el ángulo que formaban los rayos del sol con la vertical que por construcción es igual al ángulo cuyo vértice está en el centro de la Tierra (ver gráfico superior). Este ángulo resulto ser de 7º 12' ( = 7'2º) que unido al hecho conocido de que la distancia entre las dos ciudades era de 5.000 estadios, dieron como conclusión que la circunferencia de la Tierra medía 360·5000/7'2; es decir, 250.000 estadios. Aunque no se tienen datos exactos, se sabe que el estadio equivale a unos 160m (actualmente se suele tomar 158m). Por tanto, 250.000 estadios son aproximadamente 250.000*160/1000 = 40.000 Km. Esto equivale a un radio de 6.366 Km. o 6.286 si tomamos los 158m, contra los 6.371 Km. que son los admitidos hoy en día.